Levenshtein Distance (Part 3: Optimize Everything!)

In Part 1 we went through what the Levenshtein Distance is and in Part 2 we covered a few major optimizations for memory and performance. In Part 3 (this post) we will be taking things up to 11 and trying to squeeze every bit of performance out of our code.

While there are some aspects of this post that are language agnostic, this post will talk about a number of C# specific optimizations - there may be equivalent optimizations in your programming language of choice.

Being Smarter with Data

In Part 2, one of our best versions had an inner loop that looked like this:

for (var i = 1; i <= source.Length; ++i)
{
    var previousDiagonal = previousRow[0];
    var previousColumn = previousRow[0]++;

    for (var j = 1; j <= target.Length; ++j)
    {
        var insertOrDelete = Math.Min(previousColumn, previousRow[j]) + 1;
        var edit = previousDiagonal + (source[i - 1] == target[j - 1] ? 0 : 1);

        previousColumn = Math.Min(insertOrDelete, edit);
        previousDiagonal = previousRow[j];
        previousRow[j] = previousColumn;
    }
}

If you look carefully at how we are accessing some of this data, we are doing some relatively repetitive actions - specifically, how we access the "source" character for the comparison.

Each iteration of the inner-loop, we are looking up source[i - 1] which we can actually cache in the body of the outer-loop like so:

for (var i = 1; i <= source.Length; ++i)
{
    var previousDiagonal = previousRow[0];
    var previousColumn = previousRow[0]++;
    var sourceChar = source[i - 1];

    for (var j = 1; j <= target.Length; ++j)
    {
        var insertOrDelete = Math.Min(previousColumn, previousRow[j]) + 1;
        var edit = previousDiagonal + (sourceChar == target[j - 1] ? 0 : 1);

        previousColumn = Math.Min(insertOrDelete, edit);
        previousDiagonal = previousRow[j];
        previousRow[j] = previousColumn;
    }
}

While it might not be the largest performance boost, we are in the territory where every little performance boost helps.

There is another way we can be smarter here by analysing that inner-most loop logic. We are always doing 2x Math.Min calls and always adding our source-target comparison to our previousDiagonal value. These might not be the slowest operations you can run but when you run them thousands of times, it does add up.

If you shift the code around just right, we can actually cut down the number of operations in one path of our code.

for (var i = 1; i <= source.Length; ++i)
{
    var previousDiagonal = previousRow[0];
    var previousColumn = previousRow[0]++;
    var sourceChar = source[i - 1];

    for (var j = 1; j <= target.Length; ++j)
    {
        if (sourceChar == target[j - 1])
        {
            previousColumn = previousDiagonal;
        }
        else
        {
            previousColumn = Math.Min(previousColumn, previousDiagonal);
            previousColumn = Math.Min(previousColumn, previousRow[j]);
            previousColumn++;
        }

        previousDiagonal = previousRow[j];
        previousRow[j] = previousColumn;
    }
}

This change plays on the fact that when the two characters are equal, the substitution cost (aka. previousDiagonal) will be the lowest cost of the three values to compare.

Going one step further, you might notice that one path actually has two calls to previousRow[j] - we can eliminate this too with more local variables. With a bit of refactoring, it could look something like this:

for (var i = 1; i <= source.Length; ++i)
{
    var previousDiagonal = previousRow[0];
    var previousColumn = previousRow[0]++;
    var sourceChar = source[i - 1];

    for (var j = 1; j <= target.Length; ++j)
    {
        var localCost = previousDiagonal;
        var deletionCost = previousRow[j];
        if (sourceChar != target[j - 1])
        {
            localCost = Math.Min(previousColumn, localCost);
            localCost = Math.Min(deletionCost, localCost);
            localCost++;
        }
        previousColumn = localCost;
        previousRow[j] = localCost;
        previousDiagonal = deletionCost;
    }
}

These tweaks combined will amount to a decent increase in performance but we aren't done yet...

Span-ing the Memory

Memory allocations - they aren't all bad BUT if we can eliminate some, that will help us. We are dealing with strings, potentially very big strings, and depending how we handle them we can allocate a lot of memory.

In Part 2, I showed a way we can trim the strings that have equal prefixes and suffixes to give us a performance boost. This code, while works, actually isn't the best.

As a reminder, here is the piece of code I shared:

var startIndex = 0;
var sourceEnd = source.Length;
var targetEnd = target.Length;

while (startIndex < sourceEnd && startIndex < targetEnd && source[startIndex] == target[startIndex])
{
    startIndex++;
}
while (startIndex < sourceEnd && startIndex < targetEnd && source[sourceEnd - 1] == target[targetEnd - 1])
{
    sourceEnd--;
    targetEnd--;
}

var sourceLength = sourceEnd - startIndex;
var targetLength = targetEnd - startIndex;

source = source.Substring(startIndex, sourceLength);
target = target.Substring(startIndex, targetLength);

Our biggest problem here is the last two lines and their Substring call. In C#, getting a substring of another string performs another allocation equal to the length of the new string. So if we had a 500 character string being substring'd to 200 characters, we would be allocating 200 characters worth of string.

This might not be bad individually but we can do better - we can do a ZERO allocation substring by using a (relatively) new feature of C# called Span.

The most concise description I can give, Span and its comparison type ReadOnlySpan allow access to a block of memory. This block of memory might be an array, it might be a pointer or it might be a string. Accessing data in a Span is the same as accessing data in a normal array like mySpan[42]. While wrapping these various types of memory is extremely useful for safe access to data, it also has one killer function - Slice - giving us a slice of the memory without actually allocating/copying it.

To use it in our example with a string, we need to cast it to ReadOnlySpan<char> (We must use ReadOnlySpan specifically because strings are immutable). After that, we simply replace our Substring calls with their Slice equivalent.

var startIndex = 0;
var sourceEnd = source.Length;
var targetEnd = target.Length;

while (startIndex < sourceEnd && startIndex < targetEnd && source[startIndex] == target[startIndex])
{
    startIndex++;
}
while (startIndex < sourceEnd && startIndex < targetEnd && source[sourceEnd - 1] == target[targetEnd - 1])
{
    sourceEnd--;
    targetEnd--;
}

var sourceLength = sourceEnd - startIndex;
var targetLength = targetEnd - startIndex;

ReadOnlySpan<char> sourceSpan = source;
ReadOnlySpan<char> targetSpan = target;

sourceSpan = sourceSpan.Slice(startIndex, sourceLength);
targetSpan = targetSpan.Slice(startIndex, targetLength);

One caveat is that from now on, we can only deal with methods that accept ReadOnlySpan<char> so if a method only accepts string type, we would need to re-allocate our span back to a full string.

This can be one of the few downsides with these types - there are many APIs that simply don't have overloads to accept Span etc. That said, the .NET team have done a lot of work adding new overloads to accept Span or ReadOnlySpan across the entire framework.

Even with that in mind, Span has other limitations like it being stack-only, you can't store a Span on the heap (eg. as a property in a class). With what we are doing above though, Span works out perfectly.

For more information about Span, have a read of Adam Sitnik's blog post about Span.

F Pooling around with Arrays

Strings are not our only source of allocations in our code. If we look back to how we instantiate our previousRow array, that is itself an allocation.

var previousRow = new int[target.Length + 1];

Our problem is that we need this array but creating new arrays is an allocation - how do we remove this allocation? With ArrayPool of course!

Another one of the gems that have been added to .NET is sharing/renting arrays. We ask for an array of X size and we get an array at least that big. After we are done, we just return the array back to the pool for it to be used elsewhere.

While there is a lot of magic that goes on behind the scenes to make that work and scale with various size arrays, for the size arrays we can reasonably deal with, ArrayPool is a perfect fit.

So how do we use this in our code? Just two places need to change - the start and end of our code.

Start of Code

var arrayPool = ArrayPool<int>.Shared;
var previousRow = arrayPool.Rent(target.Length + 1);

End of Code

var result = previousRow[targetLength];
arrayPool.Return(pooledArray);
return result;

That's it - our array allocation is now gone thanks to the hard work of the .NET team.

There are limitations with ArrayPool like by default the array won't be empty, the array may be longer than what you rented and has a default max rent size of 1,048,576.

For more information about ArrayPool, Adam Sitnik did another great post.

Dabbling in Parallel Processing

The Levenshtein Distance algorithm isn't exactly parallel friendly. In my effort to write the fastest Levenshtein Distance implementation, I did find a brute force way to make it happen. I don't want to get your hopes up - while the code can be very fast, it is riddled with race conditions because threading is hard - this means that it won't always be correct if you run it on the same strings each time. If you have the time and patience to implement it properly, you'll certainly have one of the fastest implementations around.

Anyway, let's dig into this!

The theory goes like this - if we divide a virtual matrix by the number of cores available on the machine, we could "stagger" our calculations. Visualising this as a matrix will give you some idea of how it would work and why it is hard.

The two colours of the matrix above represent the area our threads will calculate and write to. When it comes to reading data is where the problem lies - the section on the right (blue) is dependent on the column with the letter "u" which is written to by the left side (pink). While it is certainly possible to carefully hand off from one thread to another - this is most certainly going to be the hardest part of the implementation to solve.

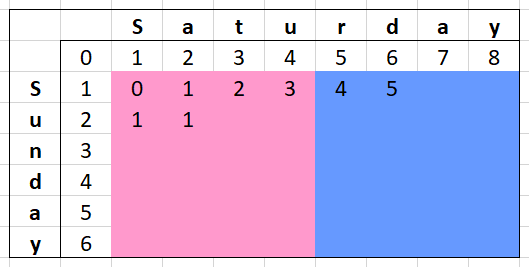
We can see above what is might look like during a parallel calculation. The left thread (pink) needs to only perform scans on the first 4 characters of "Saturday" before moving onto the next line. The thread on the right (blue) can only start if the left thread (pink) has completed that row.

This doesn't seem all bad - the left thread (pink) could run dozens of rows ahead of the right thread (blue) and we would still calculate everything correctly. In Part 2 though, we covered shrinking a full matrix down to a single row - how will that work for our parallel-ness? If we want to adopt the same optimization, it is going to make our threading a lot more complicated.

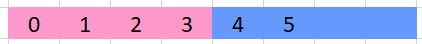
Using the row above (with our same threading colours) as an example of what our calculation row would look like. The left thread (pink) can proceed because the right thread (blue) has written its first value for that row.

Let's skip forward and say the left thread (pink) manages to fill in all its values for the next row while the right thread (blue) manages to fill one value.

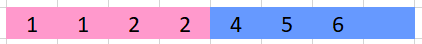
Now we are in a bit of a pickle - if the left thread (pink) manages to write another row before the right thread (blue) reads the "shared" value, it will miscalculate.

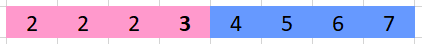
Oh no, now that shared value is 3 instead of the expected 2 - now our right thread (blue) will have the wrong insert cost when it starts the next row.

Expand this problem across bigger string comparisons with more threads and the chances of hitting this condition go up unless you have measures in place to trigger the right threads at the right time - not impossible but not trivial either.

Even with the performance bonus of a successful parallel implementation, you will be hit with performance penalities just keeping tracking of all the rows that threads are in not to mention the thread starting/stopping cost. You could (like me) just stuff threads in a while(true) loop but let's be honest, that is a bad idea.

With my (broken) implementation, for small strings it was up to 12x slower. For medium length strings (500 characters), it performed about the same as a non-parallel version. One the string length was around 8000 characters, it was performing up to 3x faster (with 8 threads) than a relatively well optimized non-parallel version.

Keeping in mind my version is flawed, that is still a significant speed boost. With more threads, bigger performance gains could likely be made.

In conclusion - I thought it would be interesting to share as a proof-of-concept but in reality, a good implementation of parallelism in Levenshtein Distance is not going to be a fun time.

Unless you have absolutely HUGE strings, I wouldn't even bother going this direction.

The Enemy of Processing: Branch Misprediction

Processors are fast using a variety of tricks with one of them being branch prediction. Put simply, it is the idea that the processor guesses whether a conditional jump will be taken or not. With its guess, it will start fetching, decoding and potentially even speculatively executing it.

It works wonders when it guesses right but when it guesses wrong, a mispredict, the processor may need to unroll and re-execute the code correctly.

All of this is important to consider given our nested for-loops - every loop performs a conditional jump (our comparison to the source or target strings). With two 1,000 character strings to compare, our inner for-loop would iterate 1,000,000 times. Two 8,000 character strings would iterate 64,000,000 times.

Earlier in this post, we covered a clever optimization to avoid our Math.Min calls - part of the benefit there wasn't avoiding just another instruction, it was avoiding a conditional jump instruction.

for (var i = 1; i <= source.Length; ++i)
{
    var previousDiagonal = previousRow[0];
    var previousColumn = previousRow[0]++;
    var sourceChar = source[i - 1];

    for (var j = 1; j <= target.Length; ++j)
    {
        var localCost = previousDiagonal;
        var deletionCost = previousRow[j];
        if (sourceChar != target[j - 1])
        {
            // The conditional jumps associated with Math.Min only execute
            // if the source character is not equal to the target character.
            localCost = Math.Min(previousColumn, localCost);
            localCost = Math.Min(deletionCost, localCost);
            localCost++;
        }
        previousColumn = localCost;
        previousRow[j] = localCost;
        previousDiagonal = deletionCost;
    }
}

Even with this in mind, we still have a lot of conditional jumps going on in our code. To take this to the next level, we will want to think about loop unrolling.

The basic premise is, cut down on the number of instructions for each iteration of the loop. In our case, we will use this to avoid our "j <= target.Length;" cost for every iteration.

for (var i = 1; i <= source.Length; ++i)
{
    var previousDiagonal = previousRow[0];
    var previousColumn = previousRow[0]++;
    var sourceChar = source[i - 1];

    var j = 1;
    var columnsRemaining = target.Length;

    int localCost;
    int deletionCost;

    while (columnsRemaining >= 8)
    {
        columnsRemaining -= 8;

        localCost = previousDiagonal;
        deletionCost = previousRow[j];
        if (sourceChar != target[j - 1])
        {
            localCost = Math.Min(previousColumn, localCost);
            localCost = Math.Min(deletionCost, localCost);
            localCost++;
        }
        previousColumn = localCost;
        previousRow[j++] = localCost;
        previousDiagonal = deletionCost;

        localCost = previousDiagonal;
        deletionCost = previousRow[j];
        if (sourceChar != target[j - 1])
        {
            localCost = Math.Min(previousColumn, localCost);
            localCost = Math.Min(deletionCost, localCost);
            localCost++;
        }
        previousColumn = localCost;
        previousRow[j++] = localCost;
        previousDiagonal = deletionCost;

        localCost = previousDiagonal;
        deletionCost = previousRow[j];
        if (sourceChar != target[j - 1])
        {
            localCost = Math.Min(previousColumn, localCost);
            localCost = Math.Min(deletionCost, localCost);
            localCost++;
        }
        previousColumn = localCost;
        previousRow[j++] = localCost;
        previousDiagonal = deletionCost;

        localCost = previousDiagonal;
        deletionCost = previousRow[j];
        if (sourceChar != target[j - 1])
        {
            localCost = Math.Min(previousColumn, localCost);
            localCost = Math.Min(deletionCost, localCost);
            localCost++;
        }
        previousColumn = localCost;
        previousRow[j++] = localCost;
        previousDiagonal = deletionCost;

        localCost = previousDiagonal;
        deletionCost = previousRow[j];
        if (sourceChar != target[j - 1])
        {
            localCost = Math.Min(previousColumn, localCost);
            localCost = Math.Min(deletionCost, localCost);
            localCost++;
        }
        previousColumn = localCost;
        previousRow[j++] = localCost;
        previousDiagonal = deletionCost;

        localCost = previousDiagonal;
        deletionCost = previousRow[j];
        if (sourceChar != target[j - 1])
        {
            localCost = Math.Min(previousColumn, localCost);
            localCost = Math.Min(deletionCost, localCost);
            localCost++;
        }
        previousColumn = localCost;
        previousRow[j++] = localCost;
        previousDiagonal = deletionCost;

        localCost = previousDiagonal;
        deletionCost = previousRow[j];
        if (sourceChar != target[j - 1])
        {
            localCost = Math.Min(previousColumn, localCost);
            localCost = Math.Min(deletionCost, localCost);
            localCost++;
        }
        previousColumn = localCost;
        previousRow[j++] = localCost;
        previousDiagonal = deletionCost;

        localCost = previousDiagonal;
        deletionCost = previousRow[j];
        if (sourceChar != target[j - 1])
        {
            localCost = Math.Min(previousColumn, localCost);
            localCost = Math.Min(deletionCost, localCost);
            localCost++;
        }
        previousColumn = localCost;
        previousRow[j++] = localCost;
        previousDiagonal = deletionCost;
    }

    if (columnsRemaining >= 4)
    {
        columnsRemaining -= 4;

        localCost = previousDiagonal;
        deletionCost = previousRow[j];
        if (sourceChar != target[j - 1])
        {
            localCost = Math.Min(previousColumn, localCost);
            localCost = Math.Min(deletionCost, localCost);
            localCost++;
        }
        previousColumn = localCost;
        previousRow[j++] = localCost;
        previousDiagonal = deletionCost;

        localCost = previousDiagonal;
        deletionCost = previousRow[j];
        if (sourceChar != target[j - 1])
        {
            localCost = Math.Min(previousColumn, localCost);
            localCost = Math.Min(deletionCost, localCost);
            localCost++;
        }
        previousColumn = localCost;
        previousRow[j++] = localCost;
        previousDiagonal = deletionCost;

        localCost = previousDiagonal;
        deletionCost = previousRow[j];
        if (sourceChar != target[j - 1])
        {
            localCost = Math.Min(previousColumn, localCost);
            localCost = Math.Min(deletionCost, localCost);
            localCost++;
        }
        previousColumn = localCost;
        previousRow[j++] = localCost;
        previousDiagonal = deletionCost;

        localCost = previousDiagonal;
        deletionCost = previousRow[j];
        if (sourceChar != target[j - 1])
        {
            localCost = Math.Min(previousColumn, localCost);
            localCost = Math.Min(deletionCost, localCost);
            localCost++;
        }
        previousColumn = localCost;
        previousRow[j++] = localCost;
        previousDiagonal = deletionCost;
    }

    while (columnsRemaining > 0)
    {
        columnsRemaining--;

        localCost = previousDiagonal;
        deletionCost = previousRow[j];
        if (sourceChar != target[j - 1])
        {
            localCost = Math.Min(previousColumn, localCost);
            localCost = Math.Min(deletionCost, localCost);
            localCost++;
        }
        previousColumn = localCost;
        previousRow[j++] = localCost;
        previousDiagonal = deletionCost;
    }
}

There is quite a bit to unpack for that code but one of the things you might be able to tell is how long some basic unrolling code might be.

while (columnsRemaining >= 8)

Our first of 3 processing chunks - we are unrolled to 8 columns of calculations at a time. This means for every loop, we've removed 7 conditional jumps that needed handling.

Once this has processed all it can, we have between 0 and 7 columns remaining for processing.

if (columnsRemaining >= 4)

In our second of 3 processing chunks, we attempt to unroll 4 columns if there are enough columns available to do so. We are removing 3 conditional jumps in this block.

Once this has processed all it can, we have between 0 and 3 columns remaining for processing.

while (columnsRemaining > 0)

In our final processing chunk, there is no unrolling - we process each item individually. At worst, we are only needing to loop through 3 columns.

The actual calculation code in each chunk is identical, just replicated the number of times needed for the given chunk.

localCost = previousDiagonal;
deletionCost = previousRow[j];
if (sourceChar != target[j - 1])
{
    localCost = Math.Min(previousColumn, localCost);
    localCost = Math.Min(deletionCost, localCost);
    localCost++;
}
previousColumn = localCost;
previousRow[j++] = localCost;
previousDiagonal = deletionCost;

This technique above, going from 8 to 4 to 1, was inspired by how the .NET runtime does this for their SpanHelpers code. While there likely was some significance to the numbers chosen for optimizing cache lines relative to the size of the code unrolled, our code likely doesn't benefit to the same extent.

One of the biggest drawbacks to applying loop unrolling like this is the dramatic increase in binary size for the same functionality, not to mention the maintenance overhead having all of those blocks repeated. A single mistake in one could break the whole calculation.

Don't even think about pushing that to its own function as function calls have overheads too unless the compiler will inline it for you!

That said, loop unrolling still provided us a net benefit if all we cared about was raw performance.

You could go further and unroll the outer loop some amount too. If done right, you would be able to minimise the number of lookups of characters in the target string. That however I will leave as an exercise to the reader.

Bonus: Using SIMD Instructions

Due in part to the extraordinary length of this post, I've split the longest part about SIMD instructions to a separate post. If you want to dive into how vectorizing CPU instructions can help us perform even faster - check it out here.

Summary

We've extracted a lot of performance out of an algorithm which isn't very performant while dramatically decreasing our memory usage.

This whole blog series about Levenshtein Distance came up purely because I wanted to build a fast and memory efficient implementation. Besides parallel support, I have actually made a version which implements every other performance feature I've talked about this series - I call it Quickenshtein!

If its not the fastest Levenshtein Distance implementation, it is surely close to it - all while allocating 0 bytes.

If .NET is your thing and this could help you, check it out. If you want to implement your own version in another language, feel free to use my implementation as a guide.

Until next time fellow readers - let your code be fast and your allocations be nil.